[Algorithm] 나머지 연산과 페르마의 소정리

이 문제를 풀며 정리한 것이다.
문제는 아래와 같이 nCr를 P로 나누었을 때, 그 값을 구하는 것이다.

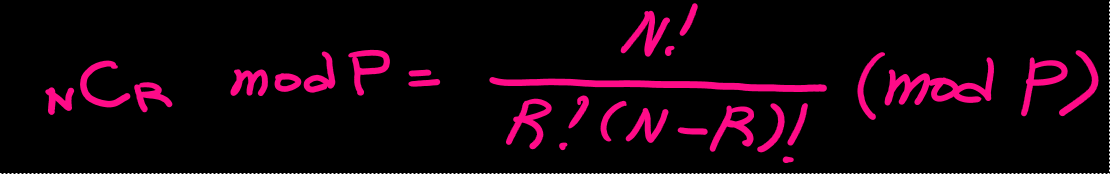
여기서 N의 값이 매우 큰 경우 모듈러의 연산을 통해 분모항과 분자항을 분리해주어야 한다.

1. 모듈러의 연산

1. a mod P + b mod P = (a+b) mod P
2. a mod P - b mod P = (a-b) mod P
3. a mod P * b mod P = (a*b) mod P

모듈러의 연산에서는 나눗셈이 없다. 그래서 분자항을 괜찮지만, 분모항을 어떻게 처리해줘야 할지 고민해야 한다.

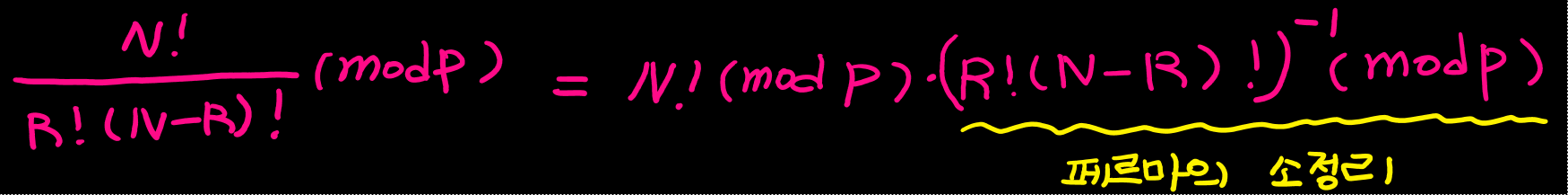
분모항을 처리하기 위해 사용하는 것이 페르마의 소정리이다.

2. 페르마의 소정리

a가 3이고, P가 5 일 때, 3의 거듭제곱을 5로 나눈 나머지는 아래와 같은 특징이 있다.

3의 거듭제곱의 나머지 규칙

이러한 규칙을 페르마의 소정리라고 하며 정확한 정의는 아래와 같다.

페르마의 소정리 정의

a가 정수, P가 소수이고, P가 a의 배수가 아니라면 아래의 공식이 성립한다.

페르마의 소정리

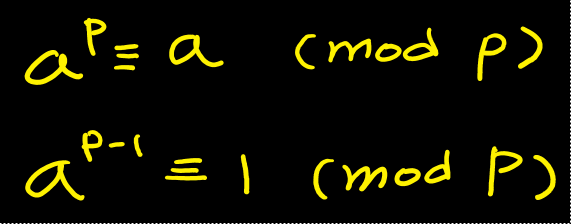
즉, (a^P) mod P를 수행하면 a가 나온다는 것이다.

페르마의 소정리를 통한 추론

페르마의 소정리를 통해 아래와 같이 추론을 할 수 있다. 이는 계산 과정에서 a^-1의 형태(분모)를 a^(P-2)로 바꿔줄 수 있다는 것이다. 만약, 계산 과정에서 쓰는 것이 아니라면 a = 3, P = 5로 계산하면 27을 5로 나눈 나머지가 1/3으로 나기때문에 꼭 계산과정에서 사용해야한다.

페르마의 소정리를 통한 추론

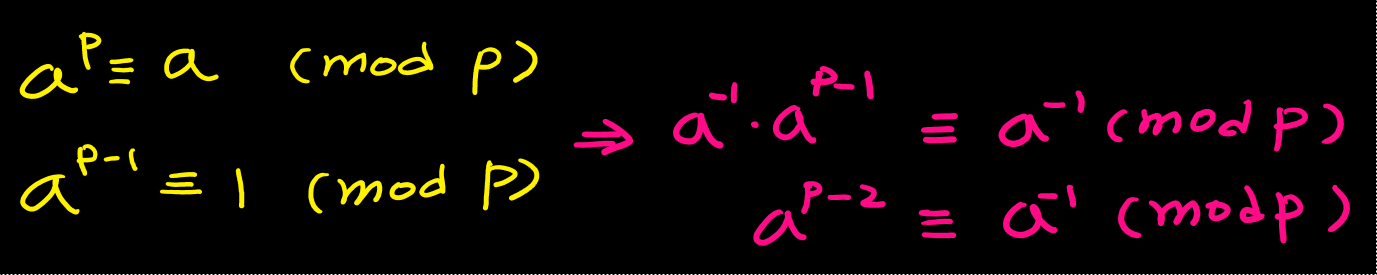
3. 이항 계수 문제 해결하기

모듈러의 연산과 페르마의 소정리를 통해 아래와 같이 식이 정해졌다.

이항 계수 연산의 식

이 식을 구현하기 위해서는 2가지가 필요하다.

• 팩토리얼 구하기
• (P-2) 제곱을 구하는 방법 : P가 매우 커서 시간 복잡도 O(P)를 해결해야 함 → 분할 정복의 이진 탐색을 이용( 시간 복잡도 O(logP) )

팩토리얼 구하기

final int MOD = 1000000007;			// P의 값
final int MAX_N = 4000000;			// N의 최대값

// 미리 모든 팩토리얼을 구해서 담음
long fac[] = new long[MAX_N + 1];		
fac[0] = 1;
for (int i = 1; i <= MAX_N; i++) fac[i] = (fac[i - 1] * i) % MOD;

이진 탐색을 통한 (P-2) 제곱 구하기

계산 중 long 범위를 넘어가는 문제가 발생하지 않도록 매 계산마다 나머지 연산을 해주어야 한다.

// x의 y제곱을 구하는 메서드
public static long power(long x, int y){        
        long result = 1l;

        while(y > 0){
            if(y % 2 == 1){     // y가 짝수면
                result = (result * x) % MOD;
            }
            y = y >> 1;         // y = y / 2
            x = (x * x) % MOD;
        }
        return result;
    }