순차적(선형) 자료구조 - 해시 테이블
어떠한 'key'값을 입력하면 'value' 값을 출력하고 싶을 땐 어떤 자료구조를 사용해야 할까요? 예를 들면, '학번'을 입력하면 '이름'을 출력하는 프로그램을 만든다고 가정해봅시다. 앞서 배운 배열에서 인덱스를 이용하여 값에 접근을 했습니다. 이 점을 이용하여 'key'를 인덱스로 하여 값에 접근할 수 없을까요? 해시 테이블을 이용하면 'key'를 이용하여 값에 접근을 할 수 있습니다.
해시 함수
해시 함수는 임의의 크기의 데이터를 고정된 크기의 값으로 매핑시켜주는 함수를 말합니다. 그래서 패스워드와 같은 민감한 데이터를 저장할 때 해시 함수를 사용하기도 합니다. 해시 함수를 사용하는 것을 '해싱(hashing)'이라고 부르기도 합니다.
자료구조의 관점에서 해시 함수는 'key'를 인덱스로 매핑하는 기능을 수행합니다. 즉, 값을 해시 테이블의 어느 인덱스에 저장해야 하는지 정하는 함수이죠.
해시 함수의 성능이 좋아야 합니다. 일반적으로 해시 함수의 충돌 가능성이 낮고(less collision), 계산이 빠른(fast computation) 함수를 성능이 좋은 함수라고 합니다. 충돌 가능성과 계산 속도는 트레이드 오프 관계이므로 적절하게 사용해야 합니다.
성능이 좋은 함수란?
less collision : 충돌이 적은 함수
fast computation : 계산이 빠른 함수
해시 테이블에 해시 값이 균일하게 분포

해시 충돌(hash collision)
해시 함수를 이용하여 구한 인덱스 위치에 이미 다른 데이터가 있는 경우에 "충돌이 일어났다."라고 합니다. 당연히 이러한 충돌이 적은 함수가 좋은 해시 함수입니다.
생일 문제
해시 함수의 충돌에 대한 대표적인 예.
여러 사람이 모였을 때 생일이 같은 사람이 2명 존재할 확률은 얼핏 봤을 때 366명이 모여야 가능할 거 같지만 23명만 모여도 50%가 넘고 57명이 넘으면 그때부터 99%를 넘어섭니다.
이렇듯 일반적인 상식과는 달리 충돌은 쉽게 일어나, 이를 최소화하는 것이 중요합니다.

해시 테이블
해시 테이블은 key와 value로 구성된 자료구조입니다. 해시 테이블을 배열로 만들어 이 배열에 value를 저장하고, 저장할 위치는 key를 해싱한 결과를 인덱스로 삼아 저장합니다. 파이썬은 이를 딕셔너리로 구현합니다.
해시 테이블의 장점으로는 매우 빠른 평균 삽입, 삭제, 탐색 연산을 제공한다는 점이 있습니다. 즉, 대부분의 연산이 O(1)에 수행됩니다. 그래서 데이터의 양에 상관없이 빠른 성능을 기대할 수 있습니다.
해시 테이블에서 value가 저장되는 배열의 공간을 slot이라고 합니다. 아래의 이미지는 총 10개의 슬롯으로 구성된 것입니다.

해시 함수의 종류
1. Perfect hash function
key와 해시 테이블의 slot이 1:1로 매칭 되는 해시 함수입니다. 그래서 충돌 가능성이 0% 이므로 매우 비현실적이고 이상적인 해시 함수입니다.

2. Universal hash function
해시 테이블의 크기(m)가 커질수록 충돌 가능성이 낮아지는 함수입니다. 설계를 하기 매우 어렵습니다.
아래는 x, y라는 두 개의 키가 존재할 때 두 키가 같을 가능성이 해시 테이블의 크기와 반비례하는 것을 수학적으로 나타낸 것입니다.

3. C-Universal hash function
이 함수는 가장 많이 사용되는 해시 함수로, Universal hash function의 설계 어려움을 해결하기 위해 만들어졌습니다. Universal 해시 함수와 유사하지만 c라는 상수값을 줘 제한을 약화시킨 함수입니다. 즉, 로드 팩터가 어느 정도 커지면 m을 증가시켜 충돌 가능성을 낮추는 방식입니다.
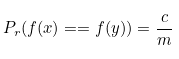
4. Division hash function
가장 단순한 해시 함수로 키를 소수로 나누는 연산을 수행합니다. 아래는 Division 해시 함수의 공식으로 슬롯 개수(m)는 소수이며 이때, 최대한 큰 소수 중 2의 거듭제곱으로 된 수와 가깝지 않은 수를 선택하는 것이 좋습니다.

5. 그 외
- Multiplication
- Folding
- Mid-squares
- Extraction
- Additive
- Rotating
충돌 회피 방법
현실적으로 해시 함수를 사용했을 때 충돌이 일어나지 않을 수 없습니다. 그렇기 때문에 만약, 충돌이 발생 시 어떤 방식으로 처리해야 고민해볼 필요가 있습니다. 회피 방법은 크게 오픈 어드레싱 방법과 개별 체이닝 방식이 있습니다.
1. Open adressing
오픈 어드레싱 방법은 충돌이 발생할 경우 그다음 슬롯부터 탐사(probing)를 시작하여 빈 슬롯을 찾는 방식입니다. 이 때문에 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장이 없습니다.
- 선형 탐사(linear probing)
해시가 충돌되면 그다음 빈 곳에 삽입하는 방식으로 오픈 어드레싱 방법 중 가장 간단한 방법입니다. 하지만 이 방법은 해시 테이블에 데이터가 고르게 분산되지 못하고 연속된 데이터 그룹이 여기저기에 생기게 됩니다. 이러한 현상을 클러스터링이라고 하는데, 이렇게 되면 탐사 시간이 증가하게 되어 해싱의 효율성을 떨어뜨리는 원인이 됩니다.
또한, 해시 테이블이 가득 차면 배열과 마찬가지로 더 큰 크기의 해시 테이블을 생성한 뒤 이를 복사해주는 과정이 필요해집니다.
- 제곱 탐사(quadratic probing)
해시가 충돌되면 f(k)+1, f(k)+4, f(k)+9, ˙˙˙, f(k)+n^2 위치 슬롯에 저장하는 방식입니다. 선형 탐사보다 클러스터의 사이즈가 작습니다.

- 이중 해싱(double hashing)
해시를 두 개 사용(f(k), g(k))하여 해시가 충돌되면 f(k)+g(k), f(k)+2g(k), f(k)+3g(k), ˙˙˙ 위치 슬롯에 저장하는 방식입니다. 해시 함수 연산을 두 번 해야 한다는 오버헤드가 존재합니다.
2. Chaining
연결 리스트를 사용하여 한 슬롯에 여러 값을 저장하는 방법을 말합니다. 연결 리스트와 오픈 어드레싱보다 간단한 알고리즘만 있으면 쉽게 구현할 수 있으므로 오픈 어드레싱보다 체이닝 방식을 선택한 언어(C++, Java, Go)들이 많습니다. 또한 해시 테이블의 가장 전통적인 구현 방식으로 흔히 해시 테이블이라고 하면 이 방식을 의미합니다.
잘 구현된 경우(로드 팩터가 낮을 경우) O(1)의 시간 복잡도를 가지지만, 모든 데이터에서 해시 충돌이 발생하는 최악의 경우, 결국 하나의 큰 연결 리스트가 되므로 O(n)의 시간 복잡도를 가집니다.

로드 팩터(Load Factor)
해시 테이블에 저장된 데이터 개수 n을 slot 개수 k로 나눈 값을 말합니다. 해시 함수의 성능 평가할 때 사용됩니다. 로드 팩터가 커질수록 해시 테이블의 성능이 감소되어, 자바의 경우 0.75가 넘어설 경우 동적 배열처럼 해시 테이블의 공간을 재할당합니다. 파이썬의 경우 로드 팩터는 0.66입니다.

오픈 어드레싱 vs 체이닝
Open addressing is preferred over chaining since the link overhead forchaining would be substantial (100% with typical malloc overhead).
파이썬은 개별 체이닝 방식을 사용하면 연결 리스트를 만들기 위해 추가 메모리 할당이 필요하고, 이 경우 속도가 느려지기 때문에 채택하지 않았습니다. 대신 오픈 어드레싱의 선형 탐사로 해시 테이블을 구현했습니다.

오픈 어드레싱의 선형 탐사의 경우 로드 팩터가 0.8, 즉, 테이블이 80% 이상 차면 급격한 성능 저하가 발생합니다. 또한, 체이닝은 무한한 값을 저장할 수 있는 반면에, 선형 탐사의 경우 테이블이 가득 차면 다른 값을 삽입하지 못합니다. 다만, 이 경우들은 모두 로드 팩터가 큰 경우일 때를 의미하고, 로드 팩터가 낮을 경우 체이닝 방식보다 효율적입니다. 그렇기 때문에 파이썬은 오픈 어드레싱 방법을 채택하고, 로드 팩터를 낮게 설정하여 해시 함수의 성능을 높이는 방법을 선택하였습니다.